# Bot check
# HW_ID: phds_sem10
# Бот проверит этот ID и предупредит, если случайно сдать что-то не то.
# Status: not final
# Перед отправкой в финальном решении удали "not" в строчке выше.
# Так бот проверит, что ты отправляешь финальную версию, а не промежуточную.
# Никакие значения в этой ячейке не влияют на факт сдачи работы.
import numpy as np
import scipy.stats as sps
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
%matplotlib inline
sns.set_style("whitegrid")
В scipy.stats распределение Стьюдента задается объектом t с параметрами:
locиscaleпараметры распределения так же как и у нормального распределениеdfчисло степеней свободы
Все остальные методы стандартные. Например, генерации выборки из распределения $T_{50}$ будет выглядеть так:
sps.t(df=50).rvs(4)
Квантили распределения Стьюдента¶
Для подсчета теоретических значений квантилей в модуле scipy.stats есть метод .ppf. На вход принимает параметр alpha - значение квантиля, а так же все параметры выбранного распределения.
sps.norm(loc=0, scale=1).ppf(0.05)
Для распределения Стьюдента нужно указать еще число степеней свобод.
sps.t(loc=0, scale=1, df=5).ppf(0.05)
Как мы видим, значения квантилей довольно сильно различаются.
Возьмите alpha равное 95% и постройте график значений квантилей распределения стьюдента $T_{n-1,(1+\alpha)/2}$ от его степеней свобод. Так же нанесите на график значение квантиля нормального распределения $z_{(1+\alpha)/2}$
Указание: рассмотрите значения степеней свобод от 1 до 50.
alpha = 0.95
dfs = <...> # массив степеней свобод
# Ваш код
Как изменяется поведение значения квантилей t распределения, есть ли у него какой-то предел?
Ответ:
ДИ в нормальной модели¶
В данном задании вам нужно изучить доверительные интервалы для параметра сдвига в нормальной модели в случае неизвестной дисперсии. Требуется построить:
- асимптотический доверительный интервал при помощи центральной предельной теоремы;
- точный неасимптотический при помощи распределений хи-квадрат, Стьюдента.
Вывод этих интервалов был разобран на лекции. Выпишите только ответы.
Асимптотический доверительный интервал:
Точный доверительный интервал:
Постройте доверительные интервалы для параметра сдвига стандартного нормального распределения. Нужно построить доверительные интервалы обоих рассмотренных выше типов. Запишите их в виде таблицы.
Указание: рассмотрите длину выборки около 20-30.
sample_size = 30
sample = <...> # выборка
asymptotic_ci = <...> # асимптотические ДИ
precise_ci = <...> # точные ДИ
Сравните полученные значения для доверительных интервалов.
Ответ:
Реализуйте функции построения этих интервалов по выборке. Функции уже задокументированы.
Интервалы считайте по префиксам. Циклы использовать запрещено. Для подсчета среднего по префиксам используйте функцию np.cumsum.
def calculate_asymptotic_confidence_intervals(sample, alpha=0.95):
'''
Функция для вычисления асимптотического доверительного интервала
параметра сдвига для всех подвыборок выборки
param sample: выборка,
param alpha: уровень доверия
return: асимптотический доверительный интервал
'''
# ваш код
return
def calculate_confidence_intervals(sample, alpha=0.95):
'''
Функция для вычисления точный доверительного интервала
параметра сдвига для всех подвыборок выборки
param sample: выборка,
param alpha: уровень доверия
return: точный доверительный интервал
'''
# ваш код
return
Сгенерируйте выборку из нормального распределения и сравните два доверительных интервала в зависимости от размера выборки. Для сравнения отобразите оба интервала на одном графике. Проследите за тем, чтобы было видно, как соотносятся размеры интервалов. Поясните теоретическую причину такого поведения доверительных интервалов.
Указание: рассмотрите длину выборки около 20-30.
Чтобы не плодить код, допишите следующую функцию (см. ниже). При выборе стиля графика помните, что если изображаются лишь точки и линии, то лучше использовать серый фон, а если присутствуют закрашенные области, то предпочтительнее белый. Графики первого типа еще называют "легкими", а второго — "тяжелыми".
Подсказка: вам может пригодиться функция plt.fill_between.
def draw_confidence_interval(
left, right, estimation=None, sample=None,
ylim=(-10, 10), color_estimation='#FF3300', color_interval='#00CC66',
color_sample='#0066FF', label_estimation='Оценка',
sample_label='Семпл', interval_label=None
):
'''
Рисует доверительный интервал и оценку в зависимости от размера выборки.
:param left: левые границы интервалов (в зависимости от n)
:param right: правые границы интервалов (в зависимости от n)
:param estimation: оценки (в зависимости от n)
:param sample: выборка
:param ylim: ограничение вертикальной оси
:param color_estimation: цвет оценки
:param color_interval: цвет интервала
:param color_sample: цвет выборки
:param label_estimation: подпись для оценки
'''
time = np.arange(len(left)) + 1
assert len(time) == len(right)
# ваш код
plt.legend(fontsize=16)
plt.ylim(ylim)
plt.xlabel('Размер выборки')
plt.title('Зависимость значений \
доверительного интервала от размера выборки')
plt.grid()
# ваш код
Вывод:
Задача 2¶
Звериный бутстреп¶
Скачайте архив animals.zip, разархивируйте его и положите в ту же папку, где лежит ноутбук. Если у вас не установлена библиотека skimage это можно сделать раскомментировав следующую ячейку.
# Установка библиотек
# ! pip install scikit-image
# ! pip install tqdm
Готово! Теперь можно начинать работу над заданием.
import numpy as np
import scipy.stats as sps
import matplotlib.pyplot as plt
import seaborn as sns
from skimage.transform import resize
from tqdm import tqdm
Изображения в numpy хранятся в виде трехмерного массива согласно RGB модели: две оси соответствуют положению пикселя на картинке, а третья — каналу. То есть для каждого пикселя мы имеем набор из трех чисел, который отвечает за интенсивность красного, зеленого и синего цветов.
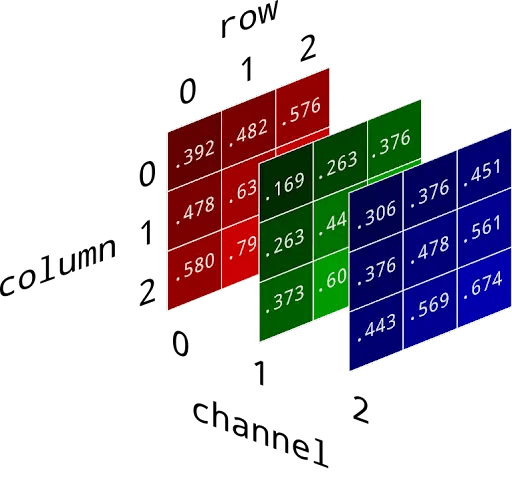
В данном задании имеется выборка, состоящая из картинок пяти зверюшек. Нужно оценить дисперсию среднего значения отдельно для каждого пикселя картинки и каждого цветового канала.
Загружаем картинки зверюшек и приводим их к размеру 500 на 500. Каждая картинка представляется в виде трехмерной матрицы размера (500, 500, 3) чисел от 0 до 1. Таким образом у нас есть выборка размера 5 из $(500\cdot500\cdot3)$-мерного пространства.
n = 5
images = [plt.imread('animals/animal_{}.jpg'.format(i + 1)) for i in range (n)]
images = [resize(images[i], (500, 500, 3)) for i in range (n)]
images[0].shape
Визуализируем все изображения при помощи функции plt.imshow(). Вызов функций plt.xticks([]), plt.yticks([]) убирает подписи к координатным осям, plt.tight_layout() обрезает пустые поля графиков, а facecolor=(0,0,0,0) делает фон графика прозрачным при сохранении (четыре числа — красный, зеленый, синий, прозрачность).
plt.figure(figsize=(10, 3))
for i in range(5):
plt.subplot(1, 5, i + 1)
plt.imshow(images[i])
plt.xticks([]), plt.yticks([])
plt.tight_layout()
plt.savefig('zoo.png', facecolor=(0,0,0,0))
plt.show()
Для визуализации в дальнейшем также загрузим изображение стрелки.
arrow = plt.imread('animals/arrow.png')
plt.figure(figsize=(3, 3))
plt.imshow(arrow)
plt.xticks([])
plt.yticks([]);
Напишем функцию, реализующую бутстреп. Вам необходимо заполнить пропуски, где они есть. Помните, что картинки — это просто трехмерные массивы, а значит на них определены все арифметические операции.
def zoo_bootstrap(images, B=6, draw=False):
'''
Генерирует B бутстрепных выборок изображений
и возвращает среднее по каждой из них.
Если указан параметр draw, то рисует процесс на графике.
'''
# размер выборки
n = len(images)
# средние по бутстрепным выборкам
bootstrap_means = []
if draw:
plt.figure(figsize=(11.5, 9.5))
for b in tqdm(range(B)):
# сумма элементов бутстрепной выборки
sum_bsample = 0
for i in range(<РАЗМЕР БУТСТРЕПНОЙ ВЫБОРКИ>):
# генерируем элемент бутстрепной выборки
ind = <сгенерируйте случайный индекс от 0 до n>
# добавляем его к сумме по этой выборке
<добавьте это изображение к сумме элементов бутстрепной выборки>
# визуализация элемента бутстрепной выборки
if draw:
plt.subplot(B, n + 2, b * (n + 2) + i + 1)
plt.imshow(images[ind])
plt.xticks([])
plt.yticks([])
if i == 0:
plt.ylabel('$X^*_{}$: '.format(b+1),
rotation=0, fontsize=26)
# добавляем среднее по бутстрепной выборке
current_mean = <посчитайте среднее по всей выборке, используя накопленную сумму sum_bsample>
bootstrap_means.append(current_mean)
if draw:
# стрелка
plt.subplot(B, n+2, b*(n+2)+i+2)
plt.imshow(arrow)
plt.axis('off'), plt.xticks([]), plt.yticks([])
# среднее по бутстрепной выборке
plt.subplot(B, n+2, b*(n+2)+i+3)
plt.imshow(bootstrap_means[-1])
plt.xticks([]), plt.yticks([])
if draw:
plt.tight_layout()
plt.savefig('animals/zoo_bootstrap.png', facecolor=(0,0,0,0))
plt.show()
return bootstrap_means
Посмотрим, что получается на выборках размера 6. Ниже будет выведена схема бутстрепа. По строкам изображены бутстрепные выборки (разумеется, размера 5). В последнем столбце по каждой бутстрепной выборке посчитано среднее всех пикселей.
bootstrap_means = zoo_bootstrap(images, draw=True)
По бутстрепной выборке средних (правый столбец выше) можем посчитать выборочную дисперсию для каждого пикселя. Поскольку цвета изображения должны быть от 0 до 1, для визуализации нормируем все дисперсии на максимальное значение по всем пикселям и цветовым каналам. Очевидно, что минимальное значение дисперсий равно нулю --- в крайних пикселях всегда белый фон.
bootstrap_var = <посчитайте дисперсию (не std) средних, полученных бутстрепом с учетом axis=0>
bvar_normed = bootstrap_var / bootstrap_var.max(axis=(0, 1)).reshape((1, 1, 3))
plt.figure(figsize=(10, 10))
plt.imshow(bvar_normed)
plt.xticks([]), plt.yticks([]);
plt.savefig('animals/zoo_bootstrap_var.png', facecolor=(0,0,0,0))
plt.show()
Посмотрим на результат при большем количестве бутстрепных выборок
bootstrap_means = zoo_bootstrap(images, B=300)
bootstrap_var = <посчитайте дисперсию (не std) средних, полученных бутстрепом с учетом axis=0>
bvar_normed = bootstrap_var / bootstrap_var.max(axis=(0, 1)).reshape((1, 1, 3))
plt.figure(figsize=(10, 10))
plt.imshow(bvar_normed)
plt.xticks([]), plt.yticks([]);
plt.savefig('animals/zoo_bootstrap_var.png', facecolor=(0,0,0,0))
plt.show()
Вывод: